Pentru a îmbunătăţi aptitudinile logico-matematice ale elevilor săi, profesorul Vasile a implementat un joc. Pe ecranul principal al jocului se afişează un şir de N scaune, numerotate de la stânga spre dreapta începând cu 1, pe fiecare scaun fiind așezat câte un copil. Fiecare copil poartă un tricou pe care este scris, de asemenea, câte un număr de la 1 la N. Numerele de pe tricouri sunt distincte și sunt scrise pe spate, deci nu sunt vizibile.

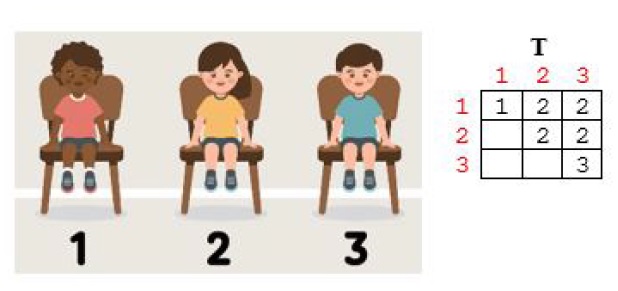
Scopul jocului este de a descoperi numărul scris pe tricoul fiecărui copil. Pentru aceasta, pe ecran mai este afişat un triunghi de numere T, care ne dă informaţii ajutătoare. Triunghiul arată ca o matrice în care liniile sunt numerotate de sus în jos de la 1 la N, iar coloanele de la stânga la dreapta de la 1 la N. Numărul scris în triunghi pe linia i şi coloana j (1 ≤ i ≤ j ≤ N) reprezintă numărul scaunului pe care stă copilul având cel mai mic număr pe tricou dintre toţi copiii situaţi pe scaune cu numere cuprinse între i şi j (inclusiv i şi j). Observaţi că poziţiile din triunghi de pe linia i şi coloana j cu 1 ≤ j < i ≤ N nu sunt completate.

Numim soluţie o succesiune de N numere naturale distincte cuprinse între 1 şi N care ar putea fi scrise, în ordine, de la stânga la dreapta, pe tricourile celor N copii, astfel încât informaţiile din triunghiul de numere să fie corecte. Două soluţii sunt considerate distincte dacă există cel puţin un copil pentru care numărul scris pe tricoul său în cele două soluţii diferă.

Cerința

Cunoscând numărul de copii şi triunghiul de numere:
1. determinați o soluţie posibilă; dacă există mai multe soluţii posibile se va afişa cea mai mică din punctul de vedere lexicografic;
2. determinați numărul de soluţii posibile.

Date de intrare

Fișierul de intrare joc.in conţine pe prima linie numărul natural C reprezentând cerinţa care trebuie să fie rezolvată (1 sau 2). Pe linia a doua se află numărul natural N cu semnificația din enunț. Pe următoarele N linii se află numerele din triunghi. Pe linia i dintre cele N sunt scrise N-i+1 numere separate prin câte un spaţiu, reprezentând numerele de pe linia i din triunghi, situate pe coloanele i, i+1, … N.

Date de ieșire

Fișierul de ieșire joc.out conţine o singură linie. Dacă C=1 linia conţine N numere naturale distincte cuprinse între 1 şi N, separate prin câte un spaţiu, reprezentând soluţia cea mai mică din punct de vedere lexicografic determinată pentru cerința 1. Dacă C=2 linia conţine numărul de soluţii posibile determinat pentru cerința 2.

Restricții și precizări

• 1 ≤ N ≤ 1000
• Spunem că șirul a[1], a[2], …, a[N] este mai mic din punctul de vedere lexicografic decât șirul b[1], b[2], …, b[N] dacă există k (1 ≤ k ≤ N), astfel încât a[i] = b[i], pentru orice 1 ≤ i < k şi a[k] < b[k].
• Se garantează că, pentru datele de test, există cel puțin o soluție.
• Pentru 9 puncte, C=1, 1 ≤ N < 10
• Pentru 9 puncte, C=2, 1 ≤ N < 10
• Pentru 22 de puncte, C=1, 10 ≤ N ≤ 1000
• Pentru 24 de puncte, C=2, 10 ≤ N < 28
• Pentru 36 de puncte, C=2, fără restricții suplimentare

Exemplul 1:

joc.in

1
3
1 2 2
2 2
3

joc.out

2 1 3

Explicație

O soluţie posibilă este 2 1 3.
Pe secvenţa de scaune 1..1 copilul cu număr minim pe tricou este pe scaunul 1.
Pe secvenţa de scaune 1..2 copilul cu număr minim pe tricou este pe scaunul 2.
Pe secvenţa de scaune 1..3 copilul cu număr minim pe tricou este pe scaunul 2.
Pe secvenţa de scaune 2..2 copilul cu număr minim pe tricou este pe scaunul 2.
Pe secvenţa de scaune 2..3 copilul cu număr minim pe tricou este pe scaunul 2.
Pe secvenţa de scaune 3..3 copilul cu număr minim pe tricou este pe scaunul 3.
O altă soluţie posibilă este 3 1 2, dar 2 1 3 este mai mică din punct de vedere lexicografic.

Exemplul 2:

joc.in

2
3
1 2 2
2 2
3

joc.out

2