Notwen a auzit de descoperirile prietenului său de pe Pământ şi a decis să studieze şi el legile gravitaţiei pe planeta sa. Pentru aceasta a conceput un experiment, care utilizează două drepte (o dreaptă verticală şi o dreaptă oblică, înclinată la un unghi oarecare faţă de orizontală) şi un super-măr (care, pentru a simplifica analiza, este considerat punctiform), ca în figură.

Super-mărul este lăsat să cadă de la o înălțime mare, de la o distanţă de x cm faţă de dreapta verticală. Super-mărul cade vertical până când întâlneşte dreapta înclinată. Când super-mărul se ciocnește de dreapta înclinată acesta sare mult în sus și spre dreapta verticală, deplasându-se astfel cu 1 cm spre dreapta verticală. Apoi, din cauza gravitaţiei, el cade din nou vertical până întâlneşte dreapta înclinată. La a doua ciocnire, super-mărul sare mult în sus și spre dreapta verticală, deplasându-se astfel cu 2 cm spre dreapta verticală. A treia oară când se ciocnește cu dreapta înclinată sare mult în sus și spre dreapta verticală, deplasându-se astfel cu 4 cm spre dreapta verticală ş.a.m.d. Notwen a observat că la fiecare ciocnire, exceptând prima, super-mărul se deplasează spre dreapta verticală cu o distanţă dublă faţă de cea de la deplasarea precedentă. Vom numi acest proces oscilaţie.

La un moment dat super-mărul se ciocnește de dreapta verticală și are loc un recul. Dacă la ultima ciocnire cu dreapta înclinată super-mărul s-a aflat la o distanță de y cm de verticală, urmând să se deplaseze cu z cm, dar y < z, acesta se va ciocni de dreapta verticală și va avea un recul de z - y cm, adică va fi “aruncat” înapoi la distanța z - y cm de dreapta verticală.

Apoi super-mărul îşi reia mişcarea în acelaşi mod, apropiindu-se de verticală la fiecare ciocnire cu dreapta înclinată mai întâi cu 1 cm, apoi cu 2 cm, 4 cm, ş.a.m.d. Studiind mişcarea super-mărului Notwen a observat că cele două procese (oscilaţie, recul) alternează până când super-mărul ajunge la distanța de 0 cm de dreapta verticală şi se opreşte.

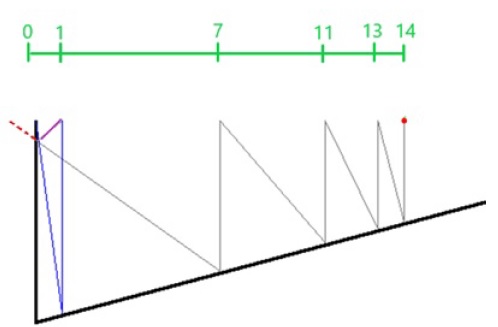
În figură este ilustrată mişcarea super-mărului pentru cazul în care experimentul începe de la o distanţă față de 14 cm de dreapta verticală. Prima oscilaţie este ilustrată cu o linie gri: super-mărul se ciocnește succesiv de dreapta înclinată la 14, 13, 11, respectiv 7 cm față de verticală, după care se ciocneşte de dreapta verticală și are un recul (ilustrat cu linie roşie) și ajunge la 8 – 7 = 1 cm de dreapta aceasta. Începe al doilea proces de oscilaţie (ilustrat cu linie albastră), dar după prima ciocnire cu dreapta înclinată se deplasează cu 1 cm spre dreapta verticală, deci ajunge chiar pe dreaptă (la 0 cm de aceasta) şi atunci se opreşte.

Cerința

Cunoscând distanţa x la care se află super-mărul față de dreapta verticală la începutul experimentului:
1. Determinați numărul de ciocniri ale super-mărului cu dreapta verticală.
2. Determinați numărul de ciocniri ale super-mărului cu dreapta înclinată.

Date de intrare

Fișierul de intrare notwen.in conţine pe prima linie numărul C reprezentând cerința care trebuie rezolvată (1 sau 2). Pe a doua linie se află numărul natural x cu semnificația din enunț.

Date de ieșire

Fișierul de ieșire notwen.out conţine o singură linie, pe care este scris numărul determinat pentru cerinţa C din fișierul de intrare.

Restricții și precizări

• 1 ≤ x ≤ 1010000
• Pentru 12 puncte, C=1, 1 ≤ x ≤ 1018
• Pentru 12 puncte, C=2, 1 ≤ x ≤ 1018
• Pentru 12 puncte, C=1, 1018 < x ≤ 10100
• Pentru 12 puncte, C=2, 1018 < x ≤ 10100
• Pentru 17 puncte, C=1, 10100 < x ≤ 101000
• Pentru 17 puncte, C=2, 10100 < x ≤ 101000
• Pentru 9 puncte, C=1, 101000 < x ≤ 1010000
• Pentru 9 puncte, C=2, 101000 < x ≤ 1010000

Exemplul 1:

notwen.in

1
14

notwen.out

2

Explicație

Vezi figura

Exemplul 2:

notwen.in

2
14

notwen.out

5

Explicație

Vezi figura

Exemplul 3:

notwen.in

1
2025

notwen.out

5

Exemplul 4:

notwen.in

2
2025

notwen.out

24

Exemplul 5:

notwen.in

1
12345678901234567890

notwen.out

42

Exemplul 6:

notwen.in

2
12345678901234567890

notwen.out

1942